Utilizando Julia para simular sistemas compostos de partes contínuas e discretas

Olá!

Nesse primeiro post, eu gostaria de explicar como eu contornei um problema que eu sempre tive relacionado com a simulação de sistemas dinâmicos que possuem partes discretas e partes contínuas. Note que com certeza esse é o território do MathWorks® Simulink. Não existe dúvida que o Simulink é a ferramenta mais rápida de prototipagem de tais tipos de aplicação em que você possui um modelo dinâmico contínuo modificado por partes discretas que são amostradas em intervalos de tempo específicos.

Entretanto, existem algumas situações em que você não consegue utilizar o Simulink (não ter uma licença é a mais óbvia). No meu caso de uso específico, eu estou codificando o simulador do Subsistema Controle de Atitude e Órbita (AOCS, em inglês) para o satélite Amazonia-1. O Simulink me deu alguns problemas relacionados com a simulação de algumas descontinuidades, como, por exemplo, sombras de algumas partes do satélite nos sensores solares. Verifiquei que eu necessitava de mais controle no solver do que o Simulink poderia me oferecer. Portanto, decidi transcrever o simulador para uma linguagem de programação “padrão”. Após um extensiva pesquisa, a linguagem Julia e o pacote OrdinaryDiffEq.jl me forneceram a melhor solução para simular o meu sistema. Portanto, neste post, gostaria de compartilhar como eu fui capaz de resolver o problema de simular sistemas com partes discretas e contínuas utilizando essas ferramentas.

Experiência necessária

Tentarei manter esse tutorial o mais simples possível. No entanto, ajudaria se você possuir um conhecimento mínimo sobre:

1. Linguagem Julia;
2. Sistemas de controle; e
3. Equações diferenciais ordinárias.

Definição do problema

Na maioria dos sistemas de controle, você possui quatro partes:

1. A planta, que é o que você quer controlar;
2. Os sensores, que medem quantidades relacionadas com os processos que você quer controlar;
3. Os atuadores, que agirão e modificarão o estado da sua planta; e
4. O controlador, que irá ler a saída dos sensores e comandará os atuadores para modificar a planta dado um conjunto de especificações.

No entanto, hoje em dia o controlador é normalmente embutido em um microcomputador, que possui intervalos pré-definidos para executar suas funções. Em outras palavras, apenas em intervalos de tempo específicos (chamados de instantes de amostragem) o controlador irá ler a saídas dos sensores, atualizar a lei de controle, e enviar novos comandos para os atuadores.

Para simular tais sistemas, você deverá considerar dois tipos de modelos: contínuos e discretos. A planta, por exemplo, é um modelo contínuo, uma vez que é normalmente modelada por um conjunto de equações diferenciais e geralmente varia para todo t. O controlador, conforme mencionado anteriormente, apenas atualiza seu estado interno em um conjunto de instantes determinados.

Academicamente falando, a simulação de um sistema desse tipo pode ser resolvida utilizando a transformada Z para converter o modelo contínuo da planta em um modelo discreto. Dessa forma, todos os modelos serão discretos e poderão ser facilmente simulados. Esse método possui muitos problemas. O maior deles, na minha opinião, é que ele funciona apenas para sistemas lineares e pode ser muito difícil de ser aplicado em plantas complexas com muitas variáveis de estado.

Portanto, o problema é: como eu posso utilizar uma linguagem de programação “padrão” para simular um sistema em que a parte contínua (a planta) é controlada por um processo discreto (o controlador)? Eu irei mostrar a seguir uma solução possível utilizando Julia e o pacote OrdinaryDiffEq.jl.

Sistema dinâmico proposto

Eu decidi propor um sistema dinâmico simples para ser controlado. Isso ajudará a tornar o tutorial mais interessante e fácil de entender. O problema que selecionei é um simples controle de uma partícula em uma dimensão definido como se segue:

Essa partícula pode ser modelada por um conjunto de duas equações diferenciais descrevendo a derivada temporal de sua posição e velocidade:

onde p é a posição da partícula, v é a velocidade da partícula e a é a aceleração da partícula, que podemos controlar.

Então, definimos o vetor de estado como:

Finalmente, nosso sistema dinâmico pode ser escrito como:

Controlador

Nós queremos controlar a aceleração de uma partícula de tal forma que ela vá para um ponto específico no espaço, chamado r. Nesse caso, eu irei propor um controlador PD (muito) simples. A lei de controle será:

O controle deverá ser executado em um processo discreto que é atualizado a cada 1s.

Nas próximas seções, eu descreverei como você poderá usar Julia e o pacote OrdinaryDiffEq.jl para simular esse sistema em uma solução muito elegante. Você verá que será capaz de facilmente estender essa ideia para lidar com sistemas muito mais complexos.

Por que eu escolhi Julia?!

No meu instituto, o INPE, eu tenho que responder quase todo dia o porquê eu escolhi Julia como a linguagem de programação para realizar meu trabalho. É um pouco difícil introduzir novas tecnologias especialmente quando você está lidando com áreas que pessoas ainda utilizam FORTRAN devido a todos aqueles códigos legados.

Eu comecei a utilizar Julia desde a versão 0.2 (estamos atualmente na versão 1.6). As razões do porquê eu realmente gostei dessa linguagem são:

1. Ela parece uma linguagem interpretada no sentido que você não precisa se preocupar com os tipos das variáveis, o que deixa um programador MATLAB bastante confortável;
2. Você pode muito facilmente chamar funções escritas em C / FORTRAN, isso é importante porque modelos como IGRF e MSIS são disponibilizados em FORTRAN;
3. O desempenho das simulações quando a vetorização é impossível (ou muito difícil) é muito melhor que o de outras linguagens interpretadas (como MATLAB, Octave, Python, etc.);
4. Você não precisa se preocupar em vetorizar o seu código;
5. Programação paralela é muito fácil de se obter; e
6. A sintaxe é muito elegante (ok, eu sei, isso é uma opinião pessoal 🙂).

Claro que existem muitos outros pontos positivos sobre Julia, por favor visite o website http://www.julialang.org para mais informações.

Além disso, para o tipo de aplicação que eu estou focando nesse tutorial, o pacote OrdinaryDiffEq.jl desenvolvido e mantido por Chris Rackauckas é único. Chris desenvolveu uma interface maravilhosa para se interagir com os solvers que deixa você fazer praticamente tudo. Conclusão: você possui todos aqueles solvers que você precisa (Runge-Kutta, Dormand-Prince, etc.) podendo interagir muito profundamente com o algoritmo para adaptá-lo às suas necessidades específicas. Devo admitir que eu não conheço nenhum outro pacote que forneça uma solução tão elegante para nenhuma outra linguagem (por favor, me avise nos comentários se eu estou me esquecendo de algo!).

Configuração

Primeiramente, faça o download do pacote Julia apropriado para o seu sistema operacional em http://www.julialang.org (note que eu testei tudo aqui utilizando Julia 1.6).

Após a instalação, abra Julia e instale o OrdinaryDiffEq.jl:

using Pkg
Pkg.add("OrdinaryDiffEq")
Pkg.add("DiffEqBase")

Para mais informações sobre esses comandos para instalar o pacote, por favor leia a documentação aqui: https://julialang.github.io/Pkg.jl/

Simulando o sistema

A primeira coisa é carregar os módulos que vamos precisar:

using DiffEqBase
using OrdinaryDiffEq

Resolver uma EDO utilizando o OrdinaryDiffEq.jl é muito similar aos outros solver disponíveis no MATLAB, por exemplo ode45. Você deverá definir uma função dinâmica, selecionar o estado inicial, ajustar algumas opções, e chamar o solver. Então, vamos definir a função dinâmica.

No OrdinaryDiffEq.jl, a função dinâmica deverá possuir a seguinte assinatura:

function f(t,u,du)

onde t é o tempo, u é o vetor de estado e du é a derivada temporal do vetor de estado. Note que u e du possuem a mesma dimensão do estado inicial. Essa função deverá computar du, mas o usuário deve ser bastante cuidadoso para não alterar a referência ao vetor! Caso contrário, o solver não irá utilizar o valor computado.

Para o nosso problema proposto, a função dinâmica será:

function dyn_eq(t,u,du)
    du .= [0 1;
           0 0]*u + [0;1]*a
end

Nota 1: Nesse exemplo, a variável de aceleração será global. Isso tornará as coisas simples, mas é um padrão de codificação muito (MUITO) ruim. Entretanto, a maneira correta de se evitar essa variável global é um pouco mais complicada e será tratada em um tutorial futuro.

Nota 2: O sinal .= significa que os valores no lado esquerdo serão copiados para o vetor du sem a alteração da referência.

Ok, nosso modelo do sistema dinâmico (a parte contínua do nosso problema) está pronto! A seguir, nós iremos codificar a lei de controle discreta.

Controlador discreto utilizando callbacks

Callbacks são um tipo de interface com o solver que faz o pacote OrdinaryDiffEq.jl ser bastante poderoso. Você define duas funções: uma para verificar se um evento ocorreu (função condição) e outra para ser executada caso esse evento tenha ocorrido (função efeito). Dessa forma, a cada instante de amostragem, o solver chama a função condição e, se ele disser que o evento ocorreu, então a função efeito é executada.

O OrdinaryDiffEq.jl provê dois tipos de Callbacks: contínuos e discretos. Nesse caso, estamos interessados em callbacks discretos em que você consegue definir precisamente antes da execução quais serão os instantes de amostragem em que a função efeito será chamada. Para maiores informações, por favor veja a documentação em https://diffeq.sciml.ai/stable/features/callback_functions/

Vamos definir primeiro a função condição para verificar se nós estamos em um intervalo de amostragem em que a lei de controle deve ser atualizada:

tf = 30.0
tstops = collect(0:1:tf)
function condition_control_loop(t,u,integrator)
    (t in tstops)
end

A variável tf define o tempo de simulação e o array tstops define os intervalos de amostragem do loop de controle. A função condition\_control\_loop, nossa função condição, simplesmente verifica se t é um dos nossos intervalos de amostragem. Se essa função retornar true, então a função efeito será executada. Note que também é possível definir uma espécie de callback baseado no vetor de estado u, mas isto não é o nosso caso.

Não se preocupe com a variável integrator. Ela basicamente define uma interface com o integrador que deixa você verificar e alterar muitas e muitas coisas. Eu irei fornecer mais informações em tutoriais futuros. Se você desejar saber mais sobre isso, verifique a documentação em https://diffeq.sciml.ai/stable/basics/integrator/

Agora, vamos definir nossa função efeito que, nesse caso, é nosso controlador:

r = 10.0
k = 0.3
d = 0.8

function control_loop!(integrator)
    global a

    p = integrator.u[1]
    v = integrator.u[2]

    a = k*(r-p) + d*(0.0-v)
end

onde r é a posição de referência e k e d são, respectivamente, os termos proporcionais e derivativos do controlador PD. Nesse caso, o loop de controle apenas necessita calcular a nova aceleração, que está escrita na variável global 😕 a, utilizando a posição e velocidade atual da partícula.

Agora, nós definiremos o callback:

cb = DiscreteCallback(condition_control_loop, control_loop!)

Executando o solver

Finalmente, precisamos apenas definir nosso estado inicial e chamar o solver do pacote OrdinaryDiffEq.jl para solucionar o problema para nós:

u0   = [0.0; 0.0]
prob = ODEProblem(dyn_eq, u0, (0.0, tf))
sol  = solve(prob, Tsit5(), callback = cb, tstops=tstops)

Tsit5()significa que estamos utilizando o método Tsitouras 5/4 Runge-Kutta. Outras soluções possíveis são DP5() para o método Dormand-Prince’s 5/4 Runge-Kutta, ou BS3() para o método Bogacki-Shampine 3/2. Todos esses métodos possuem passo de amostragem adaptativo, que é uma boa escolha para simular sistemas dinâmicos, mas você também poderá escolher métodos com passo fixo. Para maiores informações, veja a documentação em https://diffeq.sciml.ai/stable/solvers/ode_solve/

Após isto, a solução do problema será armazenada na variável sol. O vetor de tempo contendo todos os passos de amostragem aceitos pelo solver é sol.t e os vetores de estado em cada um desses instantes são armazenados em sol.u.

Se você estiver utilizando o PyPlot.jl , você poderá plotar os resultados utilizando:

plot(sol.t, sol.u)

O resultado esperado dessa simulação é:

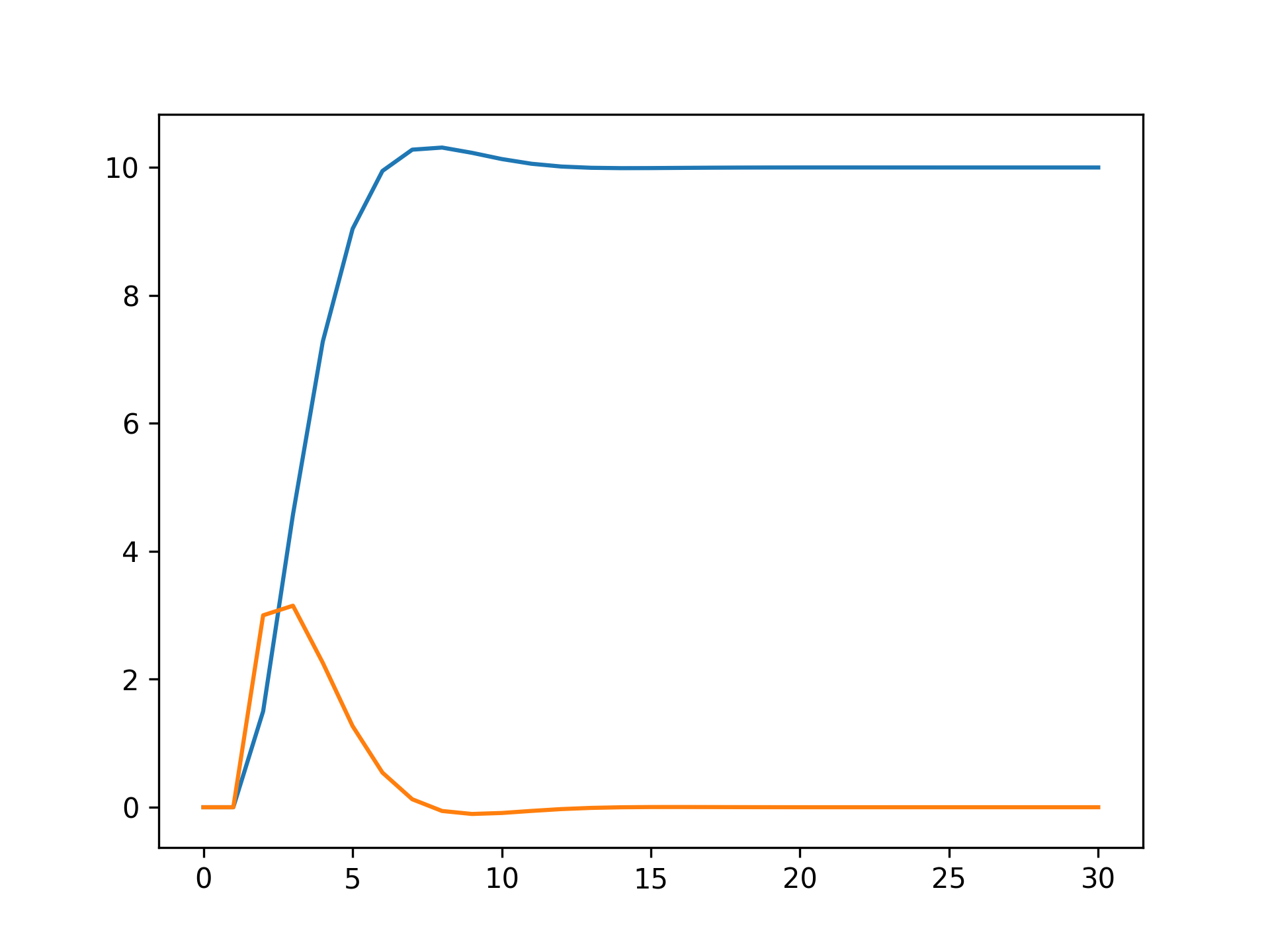
Note que pode-se ver facilmente os pontos em que o loop de controle é calculado, onde imediatamente se altera a velocidade da partícula.

Conclusão

Nesse primeiro tutorial, eu mostrei como eu utilizei Julia para simular sistemas que possuem partes contínuas e discretas. O conceito foi introduzido por um problema muito simples em que a posição de uma partícula deve ser controlada utilizando um loop de controle discreto.

Eu espero que você possa ter entendido o conceito e o quão fácil será estendê-lo para simulações muito mais complexas. Se não ficou claro, por favor, me avise nos comentário. Eu irei utilizar o seu conselho para melhorar esse e meus futuros tutoriais!

A seguir, você encontrará o código fonte desse tutorial.

using DiffEqBase
using OrdinaryDiffEq

###############################################################################
#                                  Variables
###############################################################################

# Global variable to store the acceleration.
# This solution was selected just for the sake of simplification. Don't use
# global variables!
a = 0.0

# Parameters.
r = 10.0   # Reference position.
k = 0.3    # Proportional gain.
d = 0.8    # Derivative gain.

# Configuration of the simulation.
tf     = 30.0             # Final simulation time.
tstops = collect(0:1:tf)  # Instants that the control loop will be computed.
u0     = [0.0; 0.0]       # Initial state.

###############################################################################
#                                  Functions
###############################################################################

# Dynamic equation.
function dyn_eq(du, u, p, t)
    du .= [0 1; 0 0]*u + [0;1]*a
end

# CALLBACK: Control loop.
# =======================

# Condition function.
function condition_control_loop(u, t, integrator)
    return t in tstops
end

# Affect function.
function affect_control_loop!(integrator)
    global a

    p = integrator.u[1]
    v = integrator.u[2]

    a = k*(r-p) + d*(0.0-v)
end

cb = DiscreteCallback(condition_control_loop, affect_control_loop!)

###############################################################################
#                                    Solver
###############################################################################

prob = ODEProblem(dyn_eq, u0, (0.0, tf))
sol  = solve(prob, Tsit5(), callback = cb, tstops=tstops)