O pacote SatelliteToolbox.jl para linguagem Julia

Tutorial /Julia
14 min.
Atualizado em:

Olá!

Neste tutorial, gostaria de apresentar o SatelliteToolbox.jl , que é um pacote para a linguagem Julia com muitas opções para analisar missões espaciais. Ele é usado diariamente no Instituto Nacional de Pesquisas Espaciais (INPE). Primeiramente, apresento um breve histórico sobre o pacote e, em seguida, mostro algumas análises interessantes que podem ser feitas com ele.

Histórico

Em 2013, ingressei no INPE como Engenheiro de Sistemas Espaciais Júnior. Fui designado para a divisão de sistemas espaciais onde tive que trabalhar com o subsistema de controle de atitude e órbita (AOCS). Como eu tinha apenas um conhecimento intermediário sobre órbitas, decidi me aprofundar nesse assunto codificando algoritmos e comparando os resultados com a herança do INPE e com a literatura no meu tempo livre.

O primeiro passo foi selecionar a linguagem! Em meu Doutorado, utilizei o MATLAB para simular um sistema de navegação inercial, mas as simulações de Monte Carlo eram tão lentas que precisei reescrever muitas partes em C usando CMEX. Por outro lado, na minha pesquisa de pós-doutorado, onde estudei estimação em sistemas distribuídos não-lineares, decidi usar FORTRAN (com os padrões de 2008 para ter pelo menos um código legível …) para que a velocidade de execução não fosse um problema. Sim, o desempenho foi muito bom, mas demorei muito tempo para codificar. Então ouvi falar de uma nova linguagem que prometia o melhor dos dois mundos: algo que se assemelhava a uma linguagem interpretada com a velocidade de uma linguagem compilada! E foi assim que conheci Julia .

Naquela época (usando a v0.2, eu acho), Julia era uma linguagem realmente nova. Mas decidi aceitar as dificuldades e tentar codificar meus algoritmos com ela. De qualquer forma, era apenas um pequeno projeto pessoal para aprender mais sobre órbitas. Eu enfrentei muitos bugs e até tive que usar o branch master (pre-v0.3) devido a alguns problemas e funcionalidades que não existiam, mas foi divertido 🙂.

Depois de alguns anos (e várias re-escritas devido a mudanças na linguagem), a v0.4 da linguagem Julia foi lançada. Neste momento, dada a quantidade de código que eu tinha e o estado da linguagem, comecei a ver que esse monte de algoritmos poderia, de fato, ser utilizado para auxiliar minhas atividades no INPE. Por isso, decidi criar um pacote privado, chamado SatToolbox.jl, para organizar tudo o que fiz.

Depois de algum tempo, esse pequeno projeto pessoal acabou se tornando o núcleo de um simulador do conceito operacional de missões espaciais chamado Forplan , que está sendo desenvolvido no Centro de Projeto Integrado de Missões Espaciais (CPRIME) do INPE. Dado o bom feedback que recebi, decidi renomear o pacote para SatelliteToolbox.jl e lançá-lo como um pacote oficial da linguagem Julia em março de 2018 .

Neste post, gostaria de descrever brevemente o SatelliteToolbox.jl e como ele pode ser utilizado para algumas análises relativas a missões espaciais. Todos os recursos disponíveis podem ser vistos na documentação (disponível apenas em inglês). Uma lista breve dos algoritmos implementados até o momento deste post (na v0.9.0) é:

  • Modelos atmosféricos terrestre:
  • Modelos do campo geomagnético:
  • Índices espaciais:
    • Capacidade de se obter automaticamente diversos índices espaciais, como F10.7, Ap, Kp, etc.
  • Funções para realizar análises gerais relacionadas com órbitas, como conversão de anomalias, cálculo de perturbações, etc.
  • Propagadores orbitais:
    • Two body;
    • J2;
    • J4; e
    • SGP4/SDP4.
  • Funções para converter entre sistemas de referência ECI e ECEF:
    • Toda a teoria IAU-76/FK5 é suportada. Então, a conversão entre quaisquer sistemas de referência a seguir está disponível:
      • ITRF: International Terrestrial Reference Frame;
      • PEF: Pseudo-Earth Fixed reference frame;
      • MOD: Mean-Of-Date reference frame;
      • TOD: True-Of-Date reference frame;
      • GCRF: Geocentric Celestial Reference Frame;
      • J2000: J2000 reference frame;
      • TEME: True Equator, Mean Equinox reference frame.
    • Toda a teoria IAU-2006/2010 é suportada. Então, a conversão entre quaisquer sistemas de referência a seguir está disponível:
      • ITRF: International Terrestrial Reference Frame;
      • TIRS: Terrestrial Intermediate Reference Frame;
      • CIRS: Celestial Intermediate Reference Frame;
      • GCRF: Geocentric Celestial Reference Frame.
  • Funções para converter entre referências Geocêntricas e Geodésicas (WGS-84).

A seguir, eu forneço alguns exemplos de como o SatelliteToolbox.jl pode ser utilizado para analisar missões espaciais.

Instalação

A primeira coisa a se fazer (assumindo que você já instalou Julia, que pode ser obtida aqui ) é instalar o pacote. Isso pode ser feito digitando:

julia> using Pkg
julia> Pkg.add("SatelliteToolbox")

Para carregar o pacote, que deve ser feito toda a vez que Julia é iniciada, digite:

julia> using SatelliteToolbox

Exemplos

Agora, mostrarei algumas análises que podem ser feitas com as funções que estão disponíveis.

Ano Novo na ISS

Vamos ver como podemos calcular onde os astronautas a bordo da ISS estavam durante o Ano Novo em Greenwich! A primeira coisa que devemos fazer é obter a informação sobre a órbita da ISS. Nesse caso, devemos obter o TLE (Two-Line Element), que é um formato de dados consistindo em duas linhas com 70 carácteres cada e que contém toda a informação relacionada à órbita. O TLE a seguir foi obtido do site Celestrak em 4 de Janeiro de 2019, às 12:25 (horário de Brasília).

ISS (ZARYA)             
1 25544U 98067A   19004.25252738  .00000914  00000-0  21302-4 0  9994
2 25544  51.6417  96.7089 0002460 235.6509 215.6919 15.53730820149783

Esse TLE deve ser carregado em uma variável em Julia. Existem inúmeros métodos para se fazer isso utilizando o SatelliteToolbox.jl. Aqui, utilizaremos uma string especial:

julia> iss_tle = tle"""
       ISS (ZARYA)
       1 25544U 98067A   19004.25252738  .00000914  00000-0  21302-4 0  9994
       2 25544  51.6417  96.7089 0002460 235.6509 215.6919 15.53730820149783
       """[1]
TLE:
                     Name : ISS (ZARYA)
         Satellite number : 25544
 International designator : 98067A
       Epoch (Year / Day) : 19 /   4.25252738
       Epoch (Julian Day) : 2458487.75253 (2019-01-04T06:03:38.366)
       Element set number : 999
             Eccentricity :   0.00024600 deg
              Inclination :  51.64170000 deg
                     RAAN :  96.70890000 deg
      Argument of perigee : 235.65090000 deg
             Mean anomaly : 215.69190000 deg
          Mean motion (n) :  15.53730820 revs/day
        Revolution number : 14978
                       B* : 0.000021 1/[er]
                    ṅ / 2 : 0.000009 rev/day²
                    n̈ / 6 : 0.000000 rev/day³

Esse código carrega o primeiro TLE especificado dentro da string entre tle"""...""" para a variável iss_tle.

Agora, devemos inicializar um propagador orbital utilizando o TLE carregado. Nesse caso, vamos usar o SGP4:

julia> orbp = init_orbit_propagator(Val(:sgp4), iss_tle)
OrbitPropagatorSGP4{Float64}(SGP4_Structure{Float64}
  epoch: Float64 2.45848775252738e6
  n_0: Float64 0.06779429624677841
  e_0: Float64 0.000246
  i_0: Float64 0.9013176963271556
  Ω_0: Float64 1.6878887209819442
  ω_0: Float64 4.112884090287905
  M_0: Float64 3.764533824882357
  bstar: Float64 2.1302e-5
  Δt: Float64 0.0
  a_k: Float64 1.0637096874073868
  e_k: Float64 0.000246
  i_k: Float64 0.9013176963271556
  Ω_k: Float64 1.6878887209819442
  ω_k: Float64 4.112884090287905
  M_k: Float64 3.764533824882357
  n_k: Float64 0.06778673761247853
  all_0: Float64 1.0637096874073868
  nll_0: Float64 0.06778673761247853
  AE: Float64 1.0
  QOMS2T: Float64 1.880276800610929e-9
  β_0: Float64 0.9999999697419996
  ξ: Float64 19.424864323113187
  η: Float64 0.005082954423839129
  sin_i_0: Float64 0.7841453225081563
  θ: Float64 0.6205772419196337
  θ²: Float64 0.3851161131885796
  A_30: Float64 2.53215306e-6
  k_2: Float64 0.000541314994525
  k_4: Float64 6.0412035375e-7
  C1: Float64 4.150340425449004e-10
  C3: Float64 0.005256030013878398
  C4: Float64 7.530189312128735e-7
  C5: Float64 0.0005696111334271365
  D2: Float64 1.4236674016273006e-17
  D3: Float64 7.305590907411524e-25
  D4: Float64 4.371134237708994e-32
  dotM: Float64 0.06779430410299993
  dotω: Float64 4.494429738092811e-5
  dotΩ1: Float64 -6.0376191376125836e-5
  dotΩ: Float64 -6.040900414071781e-5
  algorithm: Symbol sgp4
  sgp4_gc: SGP4_GravCte{Float64}
  sgp4_ds: SatelliteToolbox.SGP4.SGP4_DeepSpace{Float64}
)

A variável orbp agora possui a estrutura do propagador orbital do tipo SGP4 com a órbita especificada pelo TLE iss_tle. Esse TLE foi gerado no dia Juliano 2458487.75253 (2019-01-04 06:03:38.592 +0000). Portanto, devemos retro-propagar a órbita para o instante desejado 2019-01-01 00:00:00.000 +0000 (Ano Novo em Greenwich). Isso pode ser feito através da função propagate_to_epoch! como a seguir:

julia> r_teme, v_teme = propagate_to_epoch!(orbp, DatetoJD(2019, 1, 1, 0, 0, 0))
([4.611518329631408e6, -976729.067497954, -4.88282144483482e6], [-998.4098394510016, 7209.562875654184, -2387.4797255179474])

A função propagate_to_epoch! retorna três valores. O primeiro r_teme é o vetor posição e o segundo v_teme é o vetor velocidade. Esses vetores são representados no mesmo sistema de referência utilizado para descrever os elementos orbitais quando o propagador foi inicializado. Como estamos utilizando o TLE, então esses vetores estão representados no sistema de referência TEME (True Equator, Mean Equinox).

TEME é um sistema de referência inercial (ECI, Earth-Centered Inertial). Então, devemos converter o vetor posição para um sistema de referência fixo à Terra (ECEF, Earth-Centered, Earth-Fixed) para que possamos calcular a posição da ISS (latitude, longitude e altitude) no instante desejado. O SatelliteToolbox.jl possui toda a teoria IAU-76/FK5 relacionada com a conversão entre sistemas de referência . Neste exemplo, converteremos o TEME para o International Terrestrial Reference Frame (ITRF) para um cálculo mais preciso. Para esse tipo de conversão, deve-se obter os dados da orientação da Terra (EOP, Earth Orientation Data) que são fornecidos pelo IERS . O SatelliteToolbox.jl pode facilmente carregar e usar esses dados através do comando:

julia> eop = get_iers_eop()
[ Info: Downloading file 'EOP_IAU1980.TXT' from 'https://datacenter.iers.org/data/csv/finals.all.csv' with cURL.
EOPData_IAU1980:
     Data │ Timespan
 ─────────┼──────────────────────────────────────────────
        x │ 1973-01-02T00:00:00 -- 2022-06-18T00:00:00
        y │ 1973-01-02T00:00:00 -- 2022-06-18T00:00:00
  UT1-UTC │ 1973-01-02T00:00:00 -- 2022-06-18T00:00:00
      LOD │ 1973-01-02T00:00:00 -- 2021-06-09T00:00:00
       dψ │ 1973-01-02T00:00:00 -- 2021-08-24T00:00:00
       dϵ │ 1973-01-02T00:00:00 -- 2021-08-24T00:00:00

A DCM (matriz de cosenos diretores) que gira o TEME para se alinhar ao ITRF é calculada por:

julia> D_ITRF_TEME = rECItoECEF(TEME(), ITRF(), DatetoJD(2019, 1, 1, 0, 0, 0), eop)
3×3 StaticArrays.SMatrix{3, 3, Float64, 9} with indices SOneTo(3)×SOneTo(3):
 -0.179839     0.983696     4.18981e-7
 -0.983696    -0.179839    -1.3147e-6
 -1.21792e-6  -6.48585e-7   1.0

Então, o vetor posição representado no ITRF é:

julia> r_itrf = D_ITRF_TEME * r_teme
3-element StaticArrays.SVector{3, Float64} with indices SOneTo(3):
 -1.7901372297320098e6
 -4.360672082684836e6
 -4.882826427795808e6

Finalmente, considerando o elipsóide de referência WGS-84 , a latitude, longitude e altitude da ISS durante o Ano Novo em Greenwich pode ser obtida pela função ECEFtoGeodetic conforme mostrado a seguir:

julia> lat,lon,h = ecef_to_geodetic(r_itrf)
(-0.8061562372064934, -1.9603374912499567, 419859.07333969604)

julia> rad2deg(lat)
-46.18935002007934

julia> rad2deg(lon)
-112.31906466988647

julia> h/1000
419.85907333969607

ou seja, latitude 46.189° S, longitude 112.319° W e altitude 419.859 km. Isso está de acordo com o histórico disponível no website I.S.S. Tracker :

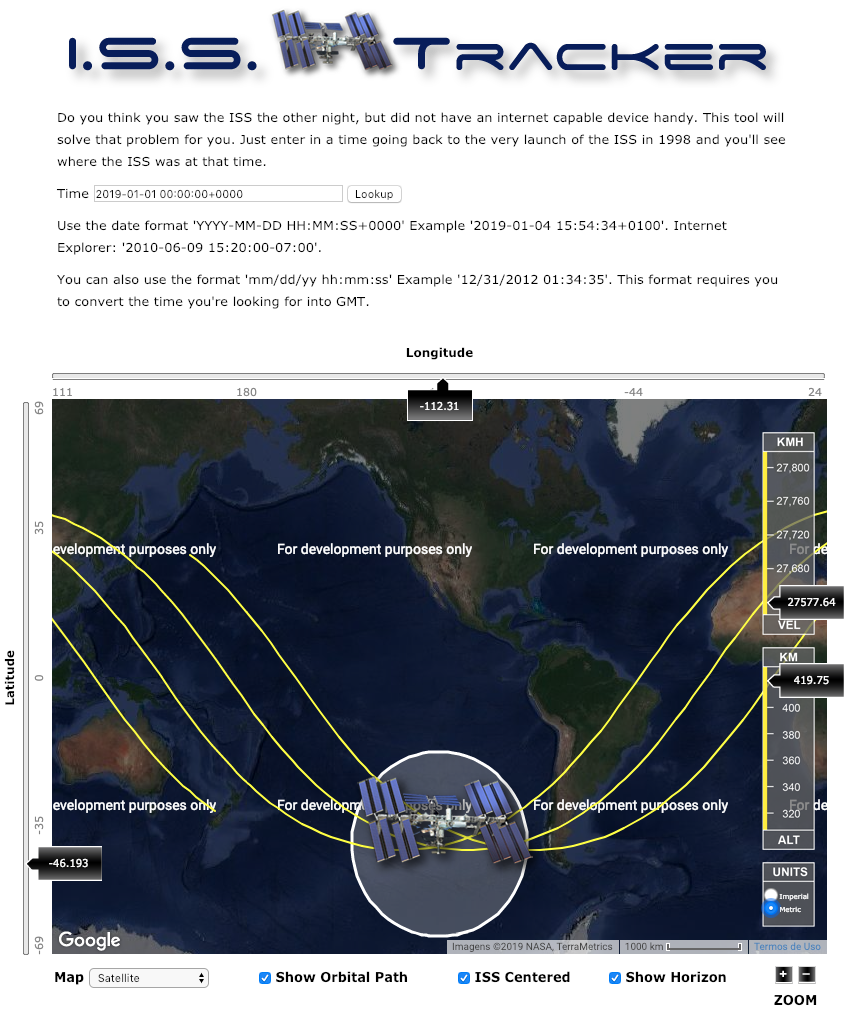
Perfil de densidade atmosférica

Neste segundo exemplo, usaremos as funções disponíveis no SatelliteToolbox.jl para calcular o perfil de densidade atmosférica. Existem muitos modelos disponíveis na literatura. O SatelliteToolbox.jl implementa quatro deles: o modelo atmosférico exponencial, o Jacchia-Roberts 1971, o Jacchia-Bowman 2008 e o NRLMSISE-00. Todos eles, exceto o primeiro, requerem como entrada alguns índices espaciais, como o F10.7, que mede a atividade do Sol, e o Ap, que mede a atividade geomagnética. O SatelliteToolbox.jl está preparado para obter todos os arquivos necessários da Internet a fim de que esses índices possam ser facilmente calculados. Isso pode ser feito por:

julia> init_space_indices(wdcfiles_newest_year = 2018)
[ Info: Downloading file 'DTCFILE.TXT' from 'http://sol.spacenvironment.net/jb2008/indices/DTCFILE.TXT' with cURL.
[ Info: Downloading file 'fluxtable.txt' from 'ftp://ftp.seismo.nrcan.gc.ca/spaceweather/solar_flux/daily_flux_values/fluxtable.txt' with cURL.
[ Info: Downloading file 'SOLFSMY.TXT' from 'http://sol.spacenvironment.net/jb2008/indices/SOLFSMY.TXT' with cURL.
[ Info: Downloading file 'kp2018.wdc' from 'ftp://ftp.gfz-potsdam.de/pub/home/obs/kp-ap/wdc/yearly/kp2018.wdc' with cURL.

Vamos calcular o perfil de densidade atmosférica de 100 km a 1000 km (passo de 1 km), utilizando todos os quatro modelos, em 2018-11-1 00: 00: 00 +0000 sobre a cidade de São José dos Campos, SP, Brasil (Latitude 23.2237 ° S, longitude 45,9009 ° W).

O modelo atmosférico exponencial, o mais simples, não depende nem dos índices espaciais nem da localização, apenas da altitude. Assim, o perfil atmosférico é calculado por:

julia> at_exp = expatmosphere.(100e3:1e3:1000e3)
901-element Vector{Float64}:
 5.297e-7
 4.4682006197154693e-7
 3.7690800034030025e-7
 3.1793478585921236e-7
 2.6818886298003355e-7
 2.2622647607479199e-7
 1.908297679051222e-7
 1.6097143424840973e-7
 1.357849088663833e-7
 1.1453921350666081e-7
 9.661e-8
 8.418342953216043e-8
 7.335524073901479e-8
 ⋮
 3.2081624552727763e-15
 3.190491541905968e-15
 3.1729179618829572e-15
 3.155441179080928e-15
 3.1380606603300916e-15
 3.1207758753974133e-15
 3.1035862969704423e-15
 3.086491400641224e-15
 3.069490664890299e-15
 3.0525835710707956e-15
 3.0357696033926073e-15
 3.019e-15

Cada elemento é a densidade atmosférica [kg / m³] relacionada a uma altitude.

Para o modelo Jacchia-Robert 2008, devemos especificar a latitude geodésica [rad], a longitude [rad] e a altitude [m]. Observe que, como já inicializamos os índices espaciais, todas as informações necessárias serão obtidas automaticamente:

julia> at_jb2008 = jb2008.(DatetoJD(2018, 11, 1, 0, 0, 0), deg2rad(-23.2237), deg2rad(-45.9009), 100e3:1e3:1000e3)
901-element Vector{JB2008_Output{Float64}}:
 JB2008_Output{Float64}
  nN2: Float64 8.667790698990597e18
  nO2: Float64 2.0068762518417774e18
  nO: Float64 6.369594178974921e17
  nAr: Float64 1.0364507121824598e17
  nHe: Float64 1.430390758033398e14
  nH: Float64 0.9692087748575587
  rho: Float64 5.33599234410689e-7
  T_exo: Float64 682.1900524076311
  Tz: Float64 193.07856649704962

 JB2008_Output{Float64}
  nN2: Float64 7.214648727684497e18
  nO2: Float64 1.64148948964543e18
  nO: Float64 5.880481385846831e17
  nAr: Float64 8.626913214258544e16
  nHe: Float64 1.1905879157579538e14
  nH: Float64 0.9677466330108101
  rho: Float64 4.441421316371682e-7
  T_exo: Float64 682.1900524076311
  Tz: Float64 195.73089787616576

 ⋮

 JB2008_Output{Float64}
  nN2: Float64 10.314784455727064
  nO2: Float64 0.008222186809865062
  nO: Float64 2.3738400239219222e7
  nAr: Float64 6.825921807010572e-9
  nHe: Float64 1.0598617834538963e11
  nH: Float64 2.1749553505283655e11
  rho: Float64 1.069027097007535e-15
  T_exo: Float64 682.1900524076311
  Tz: Float64 682.1462306202664

 JB2008_Output{Float64}
  nN2: Float64 9.948604163820175
  nO2: Float64 0.00788959257731523
  nO: Float64 2.325359614062785e7
  nAr: Float64 6.4829271673513334e-9
  nHe: Float64 1.0544232920443207e11
  nH: Float64 2.1721772409199527e11
  rho: Float64 1.0649348369412183e-15
  T_exo: Float64 682.1900524076311
  Tz: Float64 682.1464044429722

Cada elemento é uma instância da estrutura JB2008_Output que contém a densidade dos constituintes da atmosfera em [kg / m³] relacionadas a uma altitude.

O modelo NRLMSISE-00 requer as mesmas informações, mas em uma ordem diferente. Mais uma vez, como já inicializamos os índices espaciais, todas as informações necessárias são obtidas automaticamente:

julia> at_nrlmsise00 = nrlmsise00.(DatetoJD(2018, 11, 1, 0, 0, 0), 100e3:1e3:1000e3, deg2rad(-23.2237), deg2rad(-45.9009))
901-element Vector{NRLMSISE00_Output{Float64}}:
 NRLMSISE00_Output{Float64}
  den_N: Float64 3.225647667164221e11
  den_N2: Float64 1.1558415665482785e19
  den_O: Float64 4.649965500403523e17
  den_aO: Float64 4.631659520454273e-37
  den_O2: Float64 2.6263326718789934e18
  den_H: Float64 2.533162671436194e13
  den_He: Float64 1.2320073447340945e14
  den_Ar: Float64 1.1608097446818192e17
  den_Total: Float64 6.968049043353933e-7
  T_exo: Float64 1027.3184649
  T_alt: Float64 215.25904311781903
  flags: NRLMSISE00_Flags

 NRLMSISE00_Output{Float64}
  den_N: Float64 3.5691748620576013e11
  den_N2: Float64 1.0012594360559639e19
  den_O: Float64 4.6065649467733504e17
  den_aO: Float64 1.8947221849916306e-36
  den_O2: Float64 2.2358683099960123e18
  den_H: Float64 2.35052621777078e13
  den_He: Float64 1.1213184590500758e14
  den_Ar: Float64 9.845632305957742e16
  den_Total: Float64 6.029280387245405e-7
  T_exo: Float64 1027.3184649
  T_alt: Float64 213.7198609515809
  flags: NRLMSISE00_Flags

 ⋮

 NRLMSISE00_Output{Float64}
  den_N: Float64 5.1846924324256405e6
  den_N2: Float64 110.11884724745335
  den_O: Float64 7.740861835165262e7
  den_aO: Float64 2.049309406130631e9
  den_O2: Float64 0.0820328042018332
  den_H: Float64 1.3029978336346179e11
  den_He: Float64 8.29558653433061e10
  den_Ar: Float64 1.5144387918985786e-7
  den_Total: Float64 8.237307143679598e-16
  T_exo: Float64 724.4998315669409
  T_alt: Float64 724.4998315392361
  flags: NRLMSISE00_Flags

 NRLMSISE00_Output{Float64}
  den_N: Float64 5.097414213511122e6
  den_N2: Float64 106.44260908421272
  den_O: Float64 7.592117961201309e7
  den_aO: Float64 2.042142218337004e9
  den_O2: Float64 0.07891050457188623
  den_H: Float64 1.3014187084557657e11
  den_He: Float64 8.255445331597499e10
  den_Ar: Float64 1.442732462296107e-7
  den_Total: Float64 8.205713083292234e-16
  T_exo: Float64 724.4998315669409
  T_alt: Float64 724.4998315398782
  flags: NRLMSISE00_Flags

Cada elemento é uma instância da estrutura NRLMSISE00_Output que contém a densidade dos constituintes da atmosfera em [kg / m³] relacionadas a uma altitude.

O modelo Jacchia-Roberts 1971 não possui suporte à obtenção automática dos índices espaciais ainda. Portanto, precisaremos fazer isso manualmente. São necessários três índices: o F10.7 diário, a média do F10.7 (janela de 81 dias, centrada no tempo de entrada) e o índice geomagnético Kp (com um atraso de 3 horas). Essa informação pode ser obtida por:

julia> F107 = get_space_index(F10(), DatetoJD(2018, 11, 1, 0, 0, 0))
65.8

julia> F107m = get_space_index(F10M(), DatetoJD(2018, 11, 1, 0, 0, 0); window = 81)
68.29135802469136

julia> kp = get_space_index(Kp(), DatetoJD(2018, 11, 1, 0, 0, 0) - 3 / 24)
0.875

Assim, o perfil atmosférico computado por JR1971 é obtido por:

julia> at_jr1971 = jr1971.(DatetoJD(2018,11,1,0,0,0), deg2rad(-23.2237), deg2rad(-45.9009), 100e3:1e3:1000e3, F107, F107m, kp)
901-element Vector{JR1971_Output{Float64}}:
 JR1971_Output{Float64}
  nN2: Float64 5.7192521805880885e19
  nO2: Float64 1.0370130013611293e19
  nO: Float64 1.2248930040184422e19
  nAr: Float64 4.797323831280962e17
  nHe: Float64 3.150115795435398e15
  nH: Float64 0.0
  rho: Float64 3.4060767884871413e-6
  T_exo: Float64 657.167737713227
  Tz: Float64 191.2125970557249

 JR1971_Output{Float64}
  nN2: Float64 8.080629730659746e18
  nO2: Float64 1.6344357654348047e18
  nO: Float64 1.0616020508369499e18
  nAr: Float64 9.003667794720594e16
  nHe: Float64 7.366460213846506e13
  nH: Float64 0.0
  rho: Float64 4.96920849944813e-7
  T_exo: Float64 657.167737713227
  Tz: Float64 193.37386958205954

 ⋮

 JR1971_Output{Float64}
  nN2: Float64 4.99409517657604
  nO2: Float64 0.0029687873812458197
  nO: Float64 2.813594368996442e7
  nAr: Float64 1.4574247220377589e-9
  nHe: Float64 1.1029408240429312e11
  nH: Float64 3.638178032711139e11
  rho: Float64 1.3427841933298043e-15
  T_exo: Float64 669.4417264661666
  Tz: Float64 669.4417251116241

 JR1971_Output{Float64}
  nN2: Float64 4.812412406159161
  nO2: Float64 0.002845823469068375
  nO: Float64 2.7544317744479984e7
  nAr: Float64 1.3825250583995816e-9
  nHe: Float64 1.0969262471305795e11
  nH: Float64 3.63262212082261e11
  rho: Float64 1.3378408900651963e-15
  T_exo: Float64 669.4417264661666
  Tz: Float64 669.4417251377473

Cada elemento é uma instância da estrutura JR1971_Output que contém a densidade dos constituintes da atmosfera em [kg / m³] relacionadas a uma altitude.

Finalmente, utilizando o pacote PyPlot.jl , os perfis atmosféricos (altitude vs. densidade) em escala semi-log podem ser plotados usando:

julia> using PyPlot
julia> figure()
julia> h = 100:1:1000
julia> semilogx(at_exp, h, map(x->x.rho, at_jb2008), h, map(x->x.den_Total,at_nrlmsise00), h, map(x->x.rho,at_jr1971), h)
julia> legend(["Exp.", "JB2008", "NRLMSISE-00", "JR1971"])
julia> xlabel("Density [kg/m^3]")
julia> ylabel("Altitude [km]")
julia> title("Atmospheric Density, 2018-11-01 00:00:00+0000")
julia> grid()

que leva a:

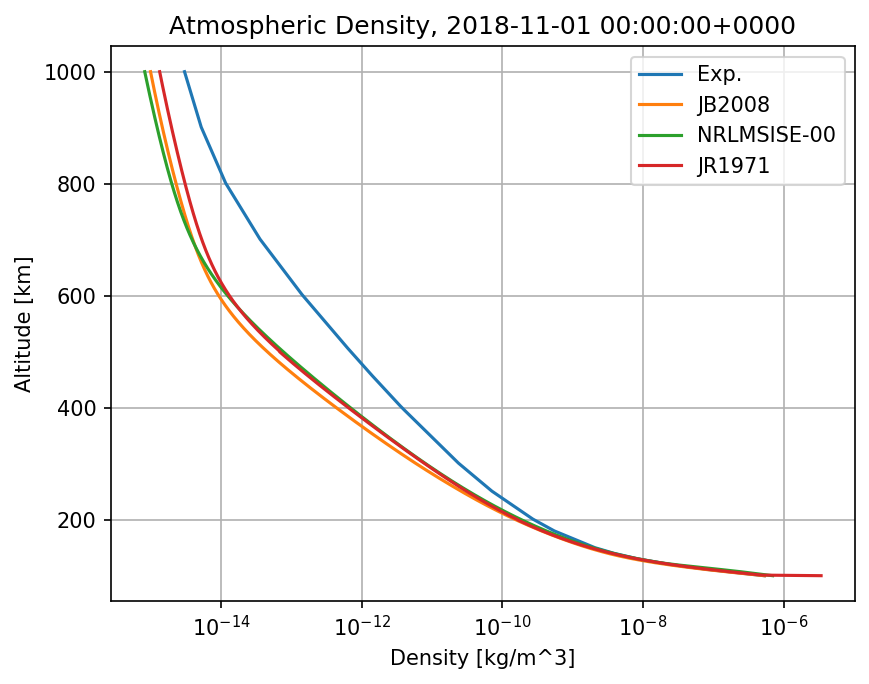
Para mais informações sobre as muitas opções para calcular a densidade atmosférica, consulte a documentação .

Conclusão

Espero que este tutorial tenha ajudado você a entender um pouco de como o pacote SatelliteToolbox.jl pode ser usado para realizar análises relacionadas a satélites e órbitas. Se você tiver alguma dúvida, por favor, fique à vontade para deixar um comentário abaixo!

#Julia
#Modelos atmosféricos
#SatelliteToolbox.jl
#Satélite
#Órbita
comments powered by Disqus